Lecture_1 Linear Regression

pd.read_csv() 用法介绍，部分用法：

  • csv文件有表头并且是第一行，那么names和header都无需指定;
  • csv文件有表头、但表头不是第一行，可能从下面几行开始才是真正的表头和数据，这个时候指定header即可;
  • csv文件没有表头，全部是纯数据，那么我们可以通过names手动生成表头;
  • csv文件有表头、但是这个表头你不想用，这个时候同时指定names和header。先用header选出表头和数据，然后再用names将表头替换掉，就等价于将数据读取进来之后再对列名进行rename；

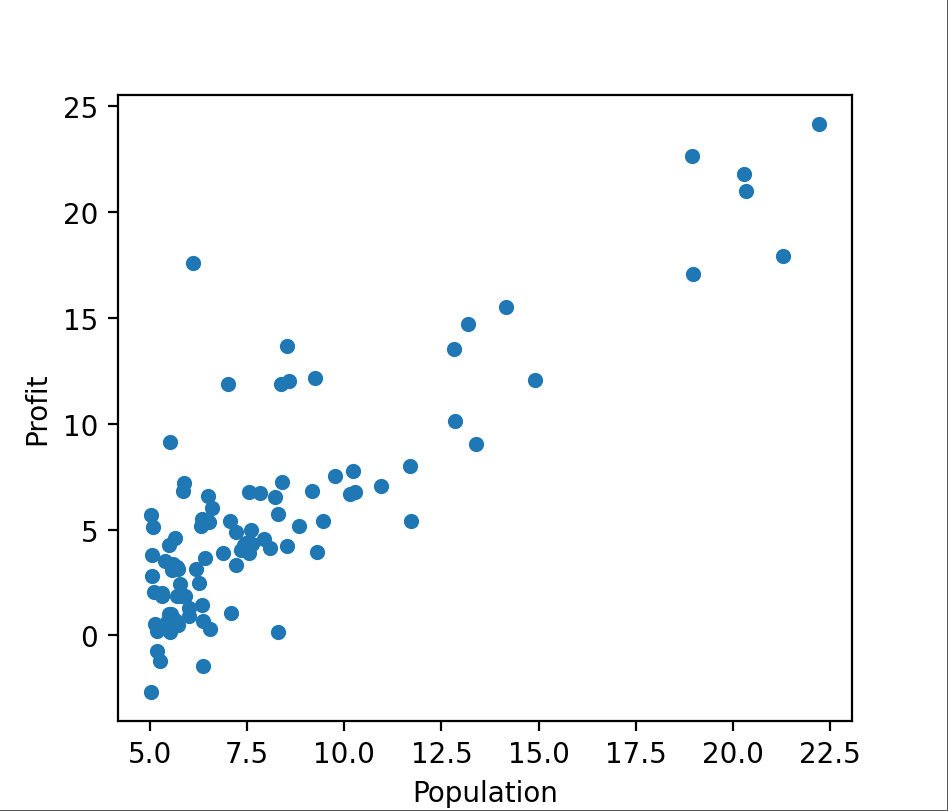
原始数据：

image-20220317175033314

使用梯度下降来实现线性回归，以最小化成本函数：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2J(\theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2

其中，hθ(x)=θTX=θ0x0+θ1x1+…+θnxnh_{\theta}(x) = \theta^{T}X=\theta_{0}x_0+\theta_1x_1+\ldots+\theta_nx_n

image-20220317175732052

image-20220318174105323

#创建数据
In [165]:data=pd.DataFrame(np.arange(16).reshape(4,4), columns=list('abcd'))
 
In [166]:data
Out[166]: 
    a   b   c   d
0   0   1   2   3
1   4   5   6   7
2   8   9  10  11
3  12  13  14  15
 
#在第一列插入一列，取名'haha'
In [167]:  data.insert(loc=0,column='haha',value=6)
 
In [168]:  data
Out[168]: 
   haha   a   b   c   d
0     6   0   1   2   3
1     6   4   5   6   7
2     6   8   9  10  11
3     6  12  13  14  15
 
#在第一列插入一列，取名'haha'（重复选择允许）
In [169]: data.insert(loc=0,column='haha',value=6，allow_duplicates=True)
 
In [170]: data
Out[170]: 
   haha  haha   a   b   c   d
0     6     6   0   1   2   3
1     6     6   4   5   6   7
2     6     6   8   9  10  11
3     6     6  12  13  14  15

image-20220318180028595

尽量不要用np.matrix()，这会让事情变得更复杂，用np.to_numpy()，以及np.dot()

batch gradient descent(批量梯度下降)

θ≔θj−∂∂θjJ(θ)\theta \coloneqq \theta_{j} - \frac{\partial}{\partial \theta_{j}}J(\theta) 

#Linear Regression
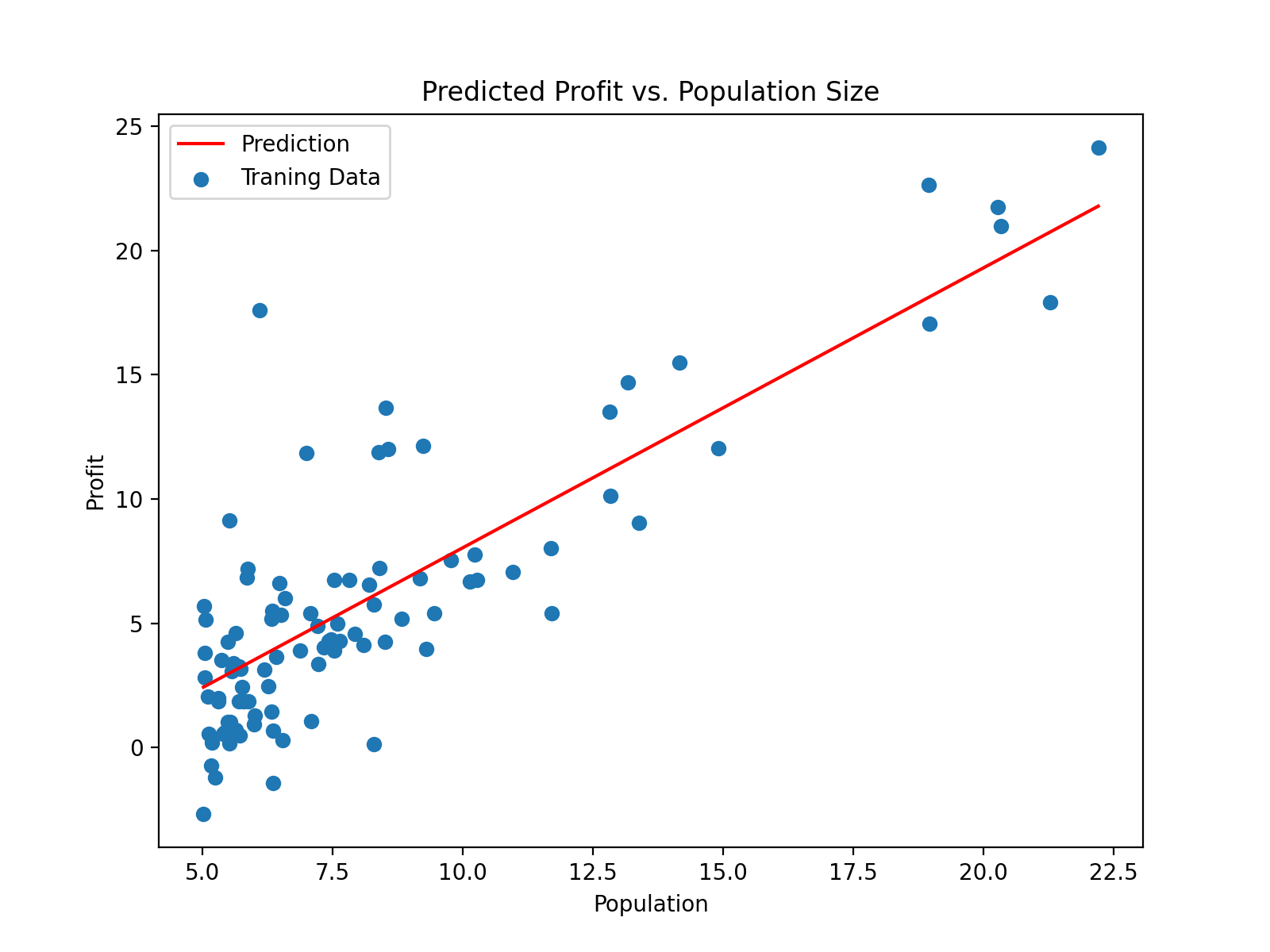
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path = 'G:/machine learning/吴恩达/学习笔记/ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
# print(data.head())
# print(data.describe())

data.plot(kind = 'scatter', x = 'Population', y = 'Profit', figsize = (8, 6))
# plt.show()

#Gradient descent
def computeCost(X, y, theta):
    error = X.dot(theta) - y
    return  (1/2 / len(X)) * np.dot(error.T, error)

data.insert(0, 'Ones', 1)

#Initialize parameters
cols = data.shape[1] #获取列数
X = data.iloc[:, 0:cols-1]
y = data.iloc[:, cols-1:]

X = X.to_numpy()
y = y.to_numpy()
theta = np.zeros((2, 1))
# print(X.shape, y.shape, theta.shape)
# print(computeCost(X, y, theta))

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.zeros(theta.shape)
    parameters = int(theta.ravel().shape[0])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X.dot(theta) - y) #X[97,2] theta[2,1], error,y [97,1]

        for j in range(parameters):
            temp_X = np.array(X[:, j]).reshape(len(X), 1)
            term = np.dot(error.T, temp_X)
            temp[j, 0] = theta[j, 0] - ((alpha / len(X)) * term)

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

#定义学习率和迭代次数
alpha = 0.01
iters = 1000

g, cost = gradientDescent(X, y, theta, alpha, iters)

x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[1, 0] * x)

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

image-20220319114738692

Linear Regression with multiple variables

#Linear Regression
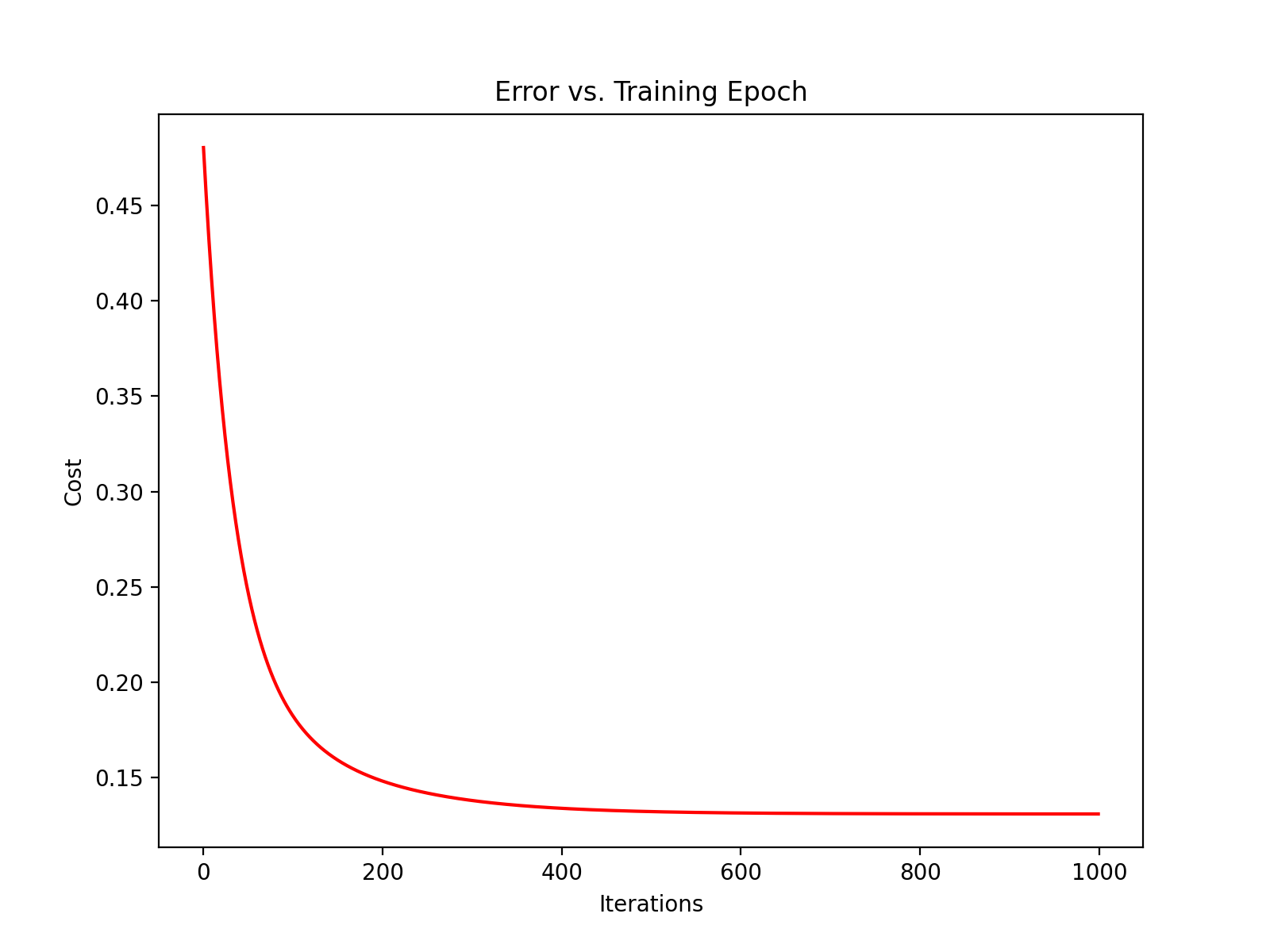
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

path = 'G:/machine learning/吴恩达/学习笔记/ex1data2.txt'
data = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
print(data.head())
# print(data.describe())

#Normalize 对数据进行归一化操作
data = (data - data.mean())/ data.std()
print(data.head())
#Gradient descent
def computeCost(X, y, theta):
    error = X.dot(theta) - y
    return  (1/2 / len(X)) * np.dot(error.T, error)

data.insert(0, 'Ones', 1)

#Initialize parameters
cols = data.shape[1] #获取列数
X = data.iloc[:, 0:cols-1]
y = data.iloc[:, cols-1:]

X = X.to_numpy()
y = y.to_numpy()
theta = np.zeros((X.shape[1], 1))
print(X.shape, y.shape, theta.shape)
# print(computeCost(X, y, theta))

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.zeros(theta.shape)
    parameters = int(theta.ravel().shape[0])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X.dot(theta) - y) #X[97,2] theta[2,1], error,y [97,1]

        for j in range(parameters):
            temp_X = np.array(X[:, j]).reshape(len(X), 1)
            term = np.dot(error.T, temp_X)
            temp[j, 0] = theta[j, 0] - ((alpha / len(X)) * term)

        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

#定义学习率和迭代次数
alpha = 0.01
iters = 1000

# perform linear regression on the data set
g, cost = gradientDescent(X, y, theta, alpha, iters)

# get the cost (error) of the model
print(computeCost(X, y, g))

fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

image-20220319115947492

使用scikit-learn的线性回归函数，而不是从头开始实现这些算法。 我们将scikit-learn的线性回归算法应用于第1部分的数据，并看看它的表现。

from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)

x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()

fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的： ∂∂θjJ(θj)=0\frac{\partial}{\partial\theta_{j}}J(\theta_{j})=0。 假设我们的训练集特征矩阵为 XX（包含了x0=1x_0 = 1）并且我们的训练集结果为向量 yy，则利用正规方程解出向量 θ=(XTX)−1XTy\theta = (X^{T}X)^{-1}X^{T}y。 上标TT代表矩阵转置，上标−1-1代表矩阵的逆。设矩阵A=XTXA=X^{T}X，则：(XTX)−1=A−1(X^{T}X)^{-1} = A^{-1}

梯度下降与正规方程的比较：

梯度下降：需要选择学习率α，需要多次迭代，当特征数量n大时也能较好适用，适用于各种类型的模型

正规方程：不需要选择学习率α，一次计算得出，需要计算(XTX)−1(X^{T}X)^{-1}，如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为O(n3)O(n^{3})，通常来说当nn小于10000 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型